Subject Area: Biology/Urban Science
A short preamble – “Three million mouse makes an elephant” is wrong – Dinner with Rev’d Malthus – How not to die in a city.
A short preamble
This essay has an underlying theme of scaling, which is to ask, how do systems respond when their size changes. A system could be a life form or a thing (such as cities or even a plank of wood).
If I am not too distracted by other essay ideas, I will love to push this idea of scaling in future writings, and I will be echoing much of the work of the theoretical physicist Geoffrey West on scaling. In the meantime, let me introduce Kleiber’s law.
“Three million mouse makes an elephant” is wrong.
The Kleiber’s rule, or what you might know as ¾ rule, states that the metabolic rate of an animal is proportional to the mass of the body raised to the power of three-quarters, mathematically expressed as the following:
B = βM^3/4 — (i)
So, what does that mean? First, metabolic rate is indicative of how much energy you need to survive. And if you happen to visit Mikumi National Park in Tanzania and ask the zookeeper for the average weight of a male African bush Elephant, she will say something like 6,000kg (~13,000lbs).
Now, compare that, for example, with a very healthy Etruscan shrew mouse which weighs – on average – 2g (~0.004lbs).
Your intuition might lead you to believe that an elephant would need something like three million times more energy to survive compared to our shrew mouse (3.25 million X 0.004lbs gives 13,000lbs).
That is, if you by any chance, plot a graph of the metabolic rate on the vertical axis and body mass of animals on the horizontal axis, what we are talking about here is a linear scaling with a line (i.e., the mathematical function) of slope 1. That is a line at an angle of 45 degrees.
To put it more colloquially, the metabolic rate increases at the same rate that the body mass increases.
Surprisingly, Max Kleiber found out that intuition was wrong – what he found was a sub-linear scaling. This means as the body mass of an animal increases, even though an increased energy level is required, they tend to use it more efficiently, thereby reducing total energy needed (a sublinear economy of scale).
Going back to graphs, if you plot metabolic rate vs. body mass of animal logarithmically; we can approximate the trend with a straight line, but now not with a slope of 1 but with a slope of ¾, which is the exponent of the power-law from equation above. This type of scaling belongs to the allometric scaling class, where the exponent of the power-law is the slope of the line when plotted.
So, again, what does this mean?
It means when animal size doubles, to keep the energy needed below 2X, the metabolic rate increases by just 75% (3/4) and not 100%. In order words, the cells are working less hard as the animal size increases.
This sub-linear scaling phenomenon can do a lot of work for us. For one, it explains why animals have bounded growth, i.e., why we grow and then stop growing.
When you take in food, the energy extracted from it is used to do work, and there are two categories of work it does, 1) growth 2) maintenance. There is less maintenance your body must do when you are a kid, so most of the energy is devoted to growth.
As you grow older, especially given the three-quarter law, less and lesser energy will be available for growth, in addition to the fact that there is much more maintenance work to be done (you have more body mass to maintain). Hence, bounded growth.
Two, it explains why we die. Specifically, why approximately rats die at age 2, dogs at 11, humans at 80. Recall that as the size of the animal increase, Kleiber’s law states that we get a 25% savings for each doubling, which is another way to restate the law.
This savings is possible because the cells work less hard. The cells take things slow if you will. Because of this, there is less wear and tear to the system, which means slower aging and a higher lifespan. Hence, humans die at 80, dogs at 11, rats at 2, roughly speaking.
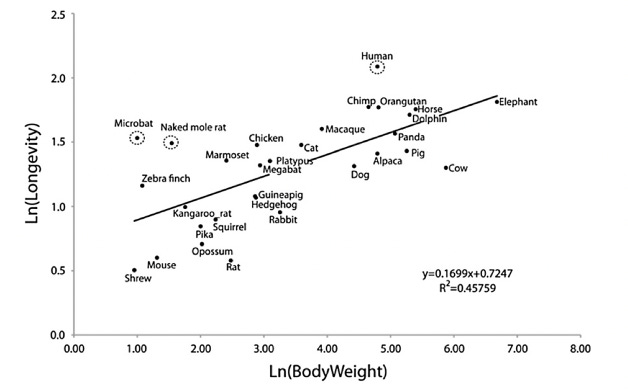
(I should also state that this scaling law is not restricted to metabolic rate and aging alone, it turns out that there is a universal quarter-power scaling law that pervades biology, and it has shown up in genome length, amount of white and gray matter of the brain, length of aorta, etc.; and this allometric scaling can be neatly explained with fractal geometry).
And what about cities?
For one, as opposed to my essay title, they do die, but they are remarkably resilient.
Let’s visit Revd. Malthus, he will be a solid segue into cities.
Dinner with Reverend Malthus
In his 1798 book – an essay on the principle of population – the 32-year-old population economist and clergyman Thomas Malthus effectively argued for a doomsday. Since it appears the world population will be growing geometrically, and food production from sedentary farming will only increase linearly, he argued, the world will end up in deep misery and hunger.
This will force humans into a subsistence economy – hunting, gathering, garbage picking, social parasitism, artisan fishing, transhumance, that kind of thing. The last time I checked the history books, Malthus was no prophet.
To quote Malthus directly:
“Famine seems to be the last, the most dreadful resource of nature. The power of population is so superior to the power of the earth to produce subsistence for man that premature death must in some shape or other visit the human race.”
– An Essay on the Principle of Population. Chapter VII, p. 61[20]

Revd. Malthus’s doomsday was supposed to have occurred, given his arguments. Little did he know everyone would be tweeting and doing Tik-Tok in 2021, while, in fact, some parts of the world would be suffering from ailments arising from eating too much food.
And here is where Malthus missed it; our grandmothers knew this very well: necessity is the mother of invention. He saw humans primarily as a liability, not as a potential asset. When I talk about assets, I talk about the agricultural revolution, the industrial revolution, the green revolution, information revolution, etc.
There are more elegant (mathematical) ways of presenting this idea. As such, a mild dose of urban science will be my next junction.
How not to Die in a City.
In a neat paper published by Geoffrey West and co-workers several years ago, they investigated scaling properties that might be found in cities. In essence, drawing an analogy between the scaling properties observed in life forms, they asked the questions: what properties of the city change as the size changes, and can these observed patterns be captured using simple equations (in a coarse-grained fashion)?
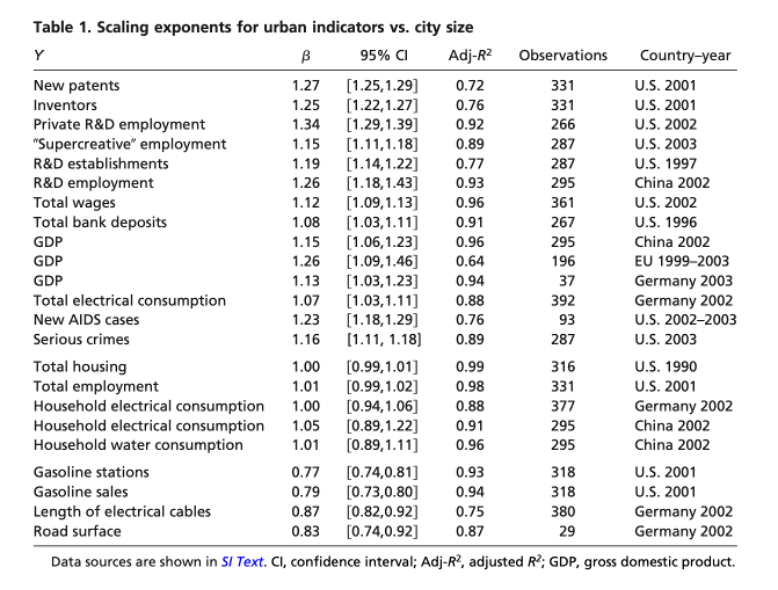
It turns out that there are, and the authors made interesting observations about cities that belong to the same urban system.
In summary, two categories of properties of cities are particularly interesting: 1) material resources that fuel the city. 2) Properties of cities that derive their essences from social interaction. The latter scales sub-linearly (slope of line/exponent of power-law < 1) while the former scales super-linearly (slope > 1).
And what are the examples?
As in biology, they reported sublinear scaling in the number of gasoline stations, gasoline sales, length of electrical cables, and road surface. In order words, as the size of cities grows bigger, say by 2X, less than 2X of these properties are needed.
On the other hand, unlike in biology, we see that patent, super-creative employment, total wages, new AIDS cases, serious crimes all scaled super-linearly. To put it in more gentle terms, say the size of a city grows by 2X; more than 2X of these properties are realized.
Very briefly, there are two things I would like to point out here:
1) The good, the bad, and the ugly come in one package: just as we get super-linear scaling benefits from innovation. More AIDS cases (and COVID-19 cases, to be more current) come with the package.
2) Revd. Malthus undone: At the risk of repeating myself, if your home city is 15 times bigger than mine, innovation in my city will be less than 15 times smaller than yours.
And the latter is precisely while cities are resilient, leading to unbounded growth. The increased innovation from more social interactions is preventing us from starving.
We die because of the sub-linear scaling that pervades our physiology; cities are resilient because of the super-linear scaling that engulfs qualities of cities associated with social currencies.
Bibliography
Geoffrey West, Scale: The Universal Laws of Life, Growth, and Death in Organisms, Cities, and Companies
Morgan et al. BMC Evolutionary Biology 2013, 13:251
Kleiber M (1947). “Body size and metabolic rate.” Physiological Reviews 27: 511–541
Bettencourt et al. PNAS April 24, 2007, 104 (17) 7301-7306




